[C++] 세 점의 각도 구하기
알고리즘

[C++] 세 점의 각도 구하기

알고리즘

이번 글에서는 세 점에서 각도를 구하는 법에 대해 알아보겠습니다.
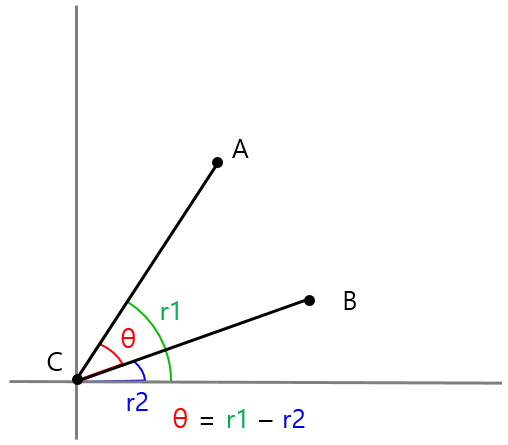
아래와 같이 세개의 점 A, B, C가 있을 때 각도θ을 구하는 방법입니다.

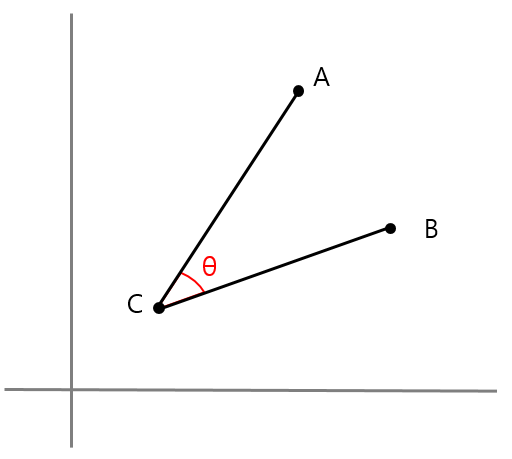
우선 각도를 구하는 방법은 tan함수를 이용하여 구할수 있습니다.
아래 그림에서 tanθ = y / x이므로 θ = atan(y / x)라는 것을 이끌어낼 수 있습니다.

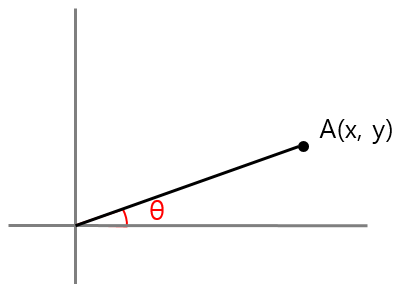
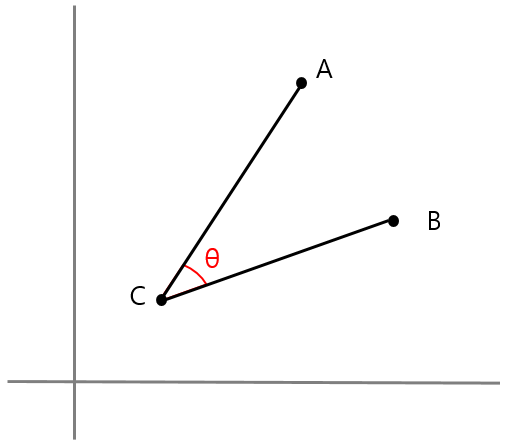
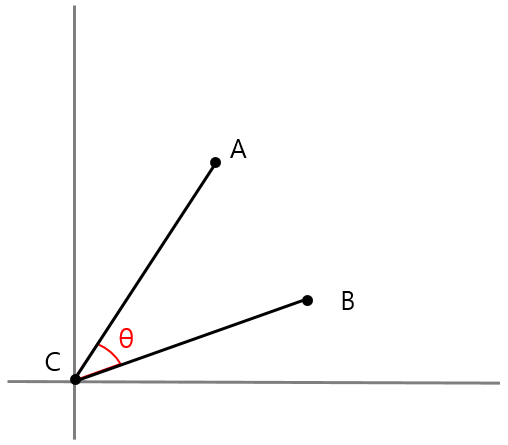
위 수식을 이용하여, 세점에서의 각도는 아래의 순서로 구할수 있습니다.

  1. 원점으로 이동한다.
  2. 직선 AC와 x축의 각도 r1을 구한다
  3. 직선 BC와 x축의 각도 r2를 구한다
  4. r1과 r2를 뺀다

이것을 코드로 아래와 같이 표현할 수 있습니다.

#include <math>

double A_X; // 점 A의 x좌표
double A_Y; // 점 A의 y좌표
double B_X; // 점 B의 x좌표
double B_Y; // 점 B의 y좌표
double C_X; // 점 C의 x좌표
double C_Y; // 점 C의 y좌표

if (!((C_X == A_X && C_Y == A_Y) || (C_X == B_X && C_Y == B_Y))) // 같은 좌표가 있으면 안된다
	double dbRadian = atan((B_Y - C_Y) / (B_X - C_X)) - atan((A_Y - C_Y) / (A_X - C_X));

이렇게 얻어낸 라디안은 호도법으로 표시된 각도이므로 우리에게 익숙한 60분법으로 변환하려면 아래와 같이 180에 π를 나누고 radian을 곱해줍니다.

#define PI 3.141592
#define DEGREE_TO_RADIAN(degree) ((PI/180)*(degree)) // 60분법 -> 호도법
#define RADIAN_TO_DEGREE(radian) ((180/PI)*(radian)) // 호도법 -> 60분법

// ...

if (!((C_X == A_X && C_Y == A_Y) || (C_X == B_X && C_Y == B_Y))) // 같은 좌표가 있으면 안된다
{
	double dbRadian = atan((B_Y - C_Y) / (B_X - C_X)) - atan((A_Y - C_Y) / (A_X - C_X));
	double dbDegree = floor(RADIAN_TO_DEGREE(dbRadian)); // floor: 반올림 함수
}

위 코드를 활용하여 아래와 같이 프로그램을 만들어 낼 수 있습니다.

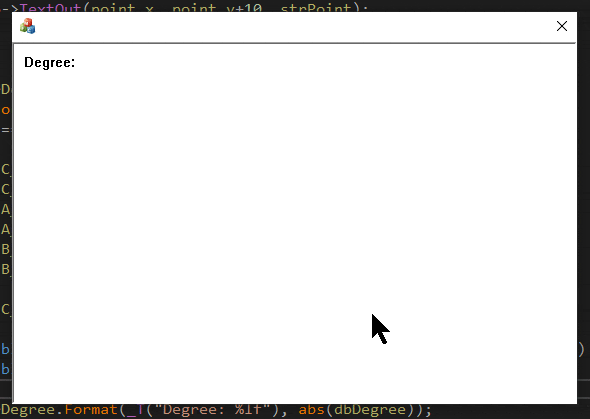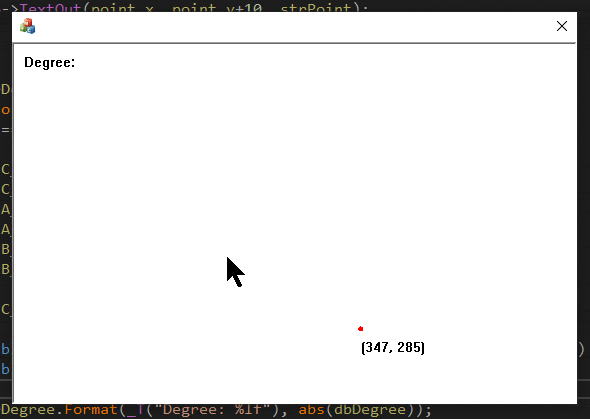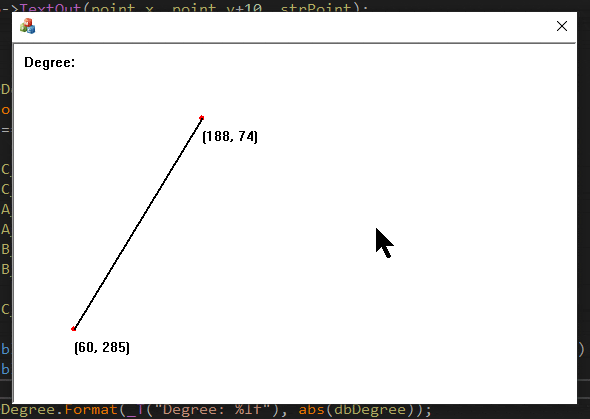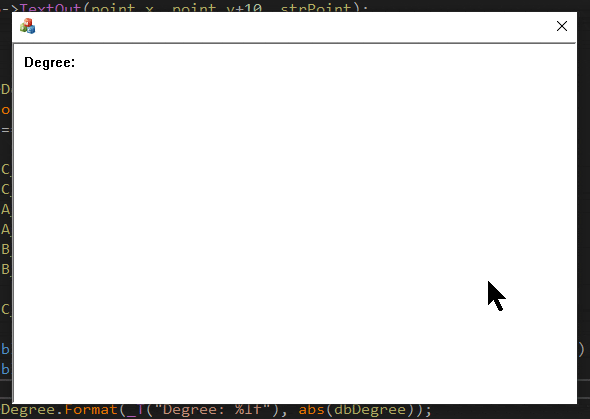
구현한 코드는 아래 코드를 다운받으면 됩니다.

3PointToDegree다운로드